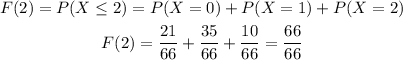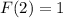Answer:
Given that,
Two balls are drawn in succession without replacement from a box containing 5 red balls and 7 black balls.
The possible outcomes and the values of the random variable X, where X is the number of red balls.
1) To find the probability distribution of the number of red balls.
Total possible outcome is
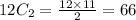
We get the X=0,1,2
If there is no red ball,
Then X=0, we get
P(X=0) is,
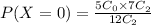
we get,
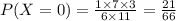
If there is 1 red ball then X=1
we get,
P(X=1) is
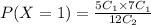
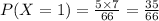
If there is 2 red balls then X=2
we get,
P(X=2) is
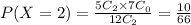
2)To find cumulative distribution function F(x)
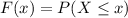
when x=0
we get,
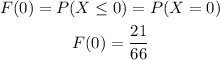
When x=1 we get
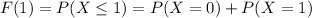
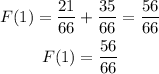
When x=2 we get,