Question

Which inequality describes the number of levels you can play in 60 minutes?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about inequalities.

Given that you have a free trial of 60 minutes of the game, it takes 5 1/6 minutes to set up the game and 7 1/3 minutes to play each level, we have to find an inequality that solves for how many levels l you can play.

Of course, if it takes 7 1/3 minutes to play each level, the amount of time spent is:

`\left(7(1)/(3)\right)\ell`

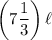
So we add it to 5 1/6, the time needed to set up the game, as follows:

`5(1)/(6)+\left(7(1)/(3)\right)\ell`

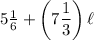
This is the total amount of time you'll spend after setting up the game and playing each level.

Since this free trial lasts for 60 minutes, then we have the inequality:

This is the answer contained in the option B.

You'll find how many levels you can play by solving the inequality. Remember the mixed fraction notation:

`a(b)/(c)=a+(b)/(c)`

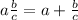
Such that you have:

`(31)/(6)+(22)/(3)\ell\leq60`

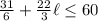
Multiply both sides of the inequality by a factor of 6

`31+44\ell\leq360`

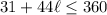
Subtract 31 on both sides of the inequality

`44\ell\leq329`

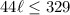
Divide both sides by a factor of 44

`\ell\leq7.47`

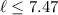
Since it has to be an integer, you can play at most 7 levels.