Given the zeros:
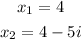
You need to remember that the Factor Theorem states that, if, for a polynomial:
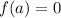
Then, this is a factor of the polynomial:

In this case, you know that:

Therefore, you can determine that these are factors of the polynomial:
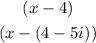
By definition, Complex Conjugates have this form:
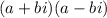
Therefore, you can determine that this is also a factor:
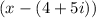
Now you can set up that the Factored Form of the polynomial is:
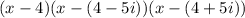
You need to expand the expression by applying the Distributive Property and applying:
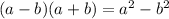
Then:
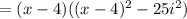
By definition:
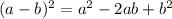
Then, you get:
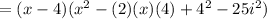
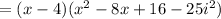
Knowing that:
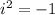
And adding the like terms, you get:
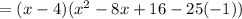
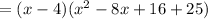
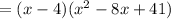
Applying the Distributive Property and adding the like terms, you get:

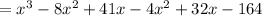
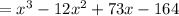
Hence, the answer is: Second option.