Question

Hello, just want to make sure my answer is correct. Thank you!

Answer 1

Given the zeros:

`\begin{gathered} x_1=4 \\ x_2=4-5i \end{gathered}`

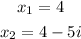
You need to remember that the Factor Theorem states that, if, for a polynomial:

`f(a)=0`

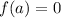
Then, this is a factor of the polynomial:

`(x-a)`

In this case, you know that:

`\begin{gathered} f(4)=0 \\ f(4-5i)=0 \end{gathered}`

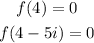
Therefore, you can determine that these are factors of the polynomial:

`\begin{gathered} (x-4) \\ (x-(4-5i)) \end{gathered}`

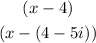
By definition, Complex Conjugates have this form:

`(a+bi)(a-bi)`

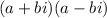
Therefore, you can determine that this is also a factor:

`(x-(4+5i))`

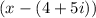
Now you can set up that the Factored Form of the polynomial is:

`(x-4)(x-(4-5i))(x-(4+5i))`

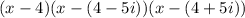
You need to expand the expression by applying the Distributive Property and applying:

`(a-b)(a+b)=a^2-b^2`

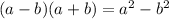
Then:

`=(x-4)((x-4)^2-25i^2)`

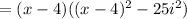
By definition:

`(a-b)^2=a^2-2ab+b^2`

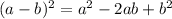
Then, you get:

`=(x-4)(x^2-(2)(x)(4)+4^2-25i^2)`
`=(x-4)(x^2-8x+16-25i^2)`

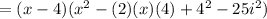
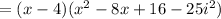
Knowing that:

`i^2=-1`

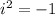
And adding the like terms, you get:

`=(x-4)(x^2-8x+16-25(-1))`
`=(x-4)(x^2-8x+16+25)`
`=(x-4)(x^2-8x+41)`

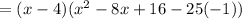
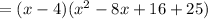
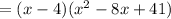
Applying the Distributive Property and adding the like terms, you get:

`=(x^2)(x)-(x)(8x)+(x)(41)-(4)(x^2)+(4)(8x)-(4)(41)`
`=x^3-8x^2+41x-4x^2+32x-164`
`=x^3-12x^2+73x-164`

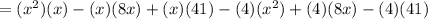
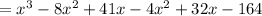
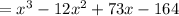
Hence, the answer is: Second option.