Question

A line goes through the points 8,16 and -2,4. (a) What is the slope of the line? Show your work.(b) Write the equation of the line in point-slope form. Show your work.(c) Write the equation of the line in slope-intercept form. Show your work.

Answer 1

ANSWERS

(a) 6/5

(b) y - 16 = 6/5(x - 8)

(c) y = 6/5x + 32/5

Step-by-step explanation

(a) The slope of a line passing through points (x₁, y₁) and (x₂, y₂) is,

`m=(y_1-y_2)/(x_1-x_2)`

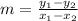
In this case, we know that the line passes through points (8, 16) and (-2, 4), so its slope is,

`m=(16-4)/(8-(-2))=(12)/(8+2)=(12)/(10)=(6)/(5)`

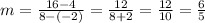
Hence, the slope of the line is 6/5.

(b) The equation of a line in point-slope form is,

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point on the line. Here, we know two points where the line passes through, so we can use either to write the equation. Using the point (8, 16),

`y-16=(6)/(5)(x-8)`

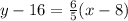
Hence, the equation of the line in point-slope form is y - 16 = 6/5(x - 8).

(c) The equation of a line in slope-intercept form is,

`y=mx+b`

Where m is the slope and b is the y-intercept.

To rewrite the equation we found in part (b) in slope-intercept form, first, apply the distributive property to the slope on the right side of the equation,

`\begin{gathered} y-16=(6)/(5)x-(6)/(5)\cdot8 \\ \\ y-16=(6)/(5)x-(48)/(5) \end{gathered}`

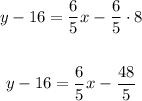
And then, add 16 to both sides,

`\begin{gathered} y-16+16=(6)/(5)x-(48)/(5)+16 \\ \\ y=(6)/(5)x+(32)/(5) \end{gathered}`

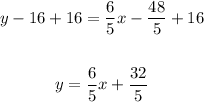
Hence, the equation in slope-intercept form is y = 6/5x + 32/5.