ANSWERS
(a) 6/5
(b) y - 16 = 6/5(x - 8)
(c) y = 6/5x + 32/5
Step-by-step explanation
(a) The slope of a line passing through points (x₁, y₁) and (x₂, y₂) is,
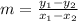
In this case, we know that the line passes through points (8, 16) and (-2, 4), so its slope is,

Hence, the slope of the line is 6/5.
(b) The equation of a line in point-slope form is,

Where m is the slope and (x₁, y₁) is a point on the line. Here, we know two points where the line passes through, so we can use either to write the equation. Using the point (8, 16),
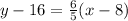
Hence, the equation of the line in point-slope form is y - 16 = 6/5(x - 8).
(c) The equation of a line in slope-intercept form is,

Where m is the slope and b is the y-intercept.
To rewrite the equation we found in part (b) in slope-intercept form, first, apply the distributive property to the slope on the right side of the equation,
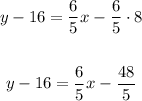
And then, add 16 to both sides,
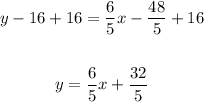
Hence, the equation in slope-intercept form is y = 6/5x + 32/5.