Question

Show how to find the inverse of f(x)=x^3-5. Calculate 3 points on f(x) and use these points to show that the inverse is correct

Answer 1

Step 1

Given;

`f(x)=x^3-5`

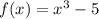
Required; To find the inverse of f(x)

Step 2

Find the inverse

`\begin{gathered} let\text{ y=f\lparen x\rparen} \\ y=x^3-5 \\ replace\text{ y with x and x with y} \\ x=y^3-5 \end{gathered}`

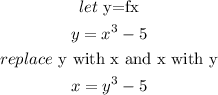
Then solve for y

`\begin{gathered} x=y^3-5 \\ y^3=x+5 \\ Take\text{ cube root of both sides} \\ \sqrt[3]{y^3}=\sqrt[3]{x+5} \\ y=\sqrt[3]{x+5} \end{gathered}`

Hence,

`f^(-1)(x)=\sqrt[3]{x+5}`

Step 3

Choose 3 points on f(x) and use these points to show that the inverse is correct.

The 3 points are;

`(2,3),\text{ \lparen0,-5\rparen, \lparen-2,-13\rparen}`
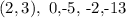
`\begin{gathered} f^(-1)(x)=\sqrt[3]{x+5} \\ (2,3),\text{ where for inverse x=3, y=2} \\ f^(-1)(x)=\sqrt[3]{3+5} \\ f^(-1)(x)=2 \end{gathered}`
`\begin{gathered} f^(-1)(x)=\sqrt[3]{x+5} \\ (0,-5) \\ f^(-1)(x)=\sqrt[3]{-5+5} \\ f^(-1)(x)=0 \end{gathered}`
`\begin{gathered} f^(-1)(x)=\sqrt[3]{(x+5)} \\ (-2,-13) \\ f^(-1)(x)=\sqrt[3]{-13+5} \\ f^(-1)(x)=\sqrt[3]{-8}=-\sqrt[3]{8}=-2 \end{gathered}`

Hence, having seen that when we substitute y for x from the points from f(x), we get x for y from f(x), the inverse is correct.