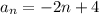Given the table:
x y
1 2
2 0
3 -2
4 -4
Difference between x values:
4 - 3 = 1
3 - 2 = 1
2 - 1 = 1
Difference between y values:
-4 - - 2 = -4 + 2 = -2
-2 - - 0 = - 2 + 0 = -2
0 - 2 = -2
This table represents an Arithmetic sequence.
An arithmetic sequence is a sequence that has a constant difference between the terms.
From the table given, the difference between the consecutive terms is constant.
We have:
First term = 2
Second term = 0
Third term = -2
Fourth term = -4
Arithmetic sequence has a common difference.
The common difference = -2
Use the arithmetic sequence formula:

Where:
a1 = first term
n = number of terms
d = common difference
To write the recursive formula, we have:
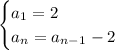
To write the explicit formula, we have:
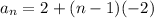
Let's simplify the explicit formula:
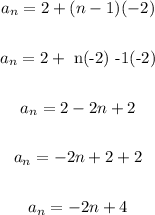
To find the 10th term, let's use the explicit formula.
Substitute 10 for n
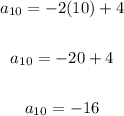
Therefore, the 10th term of the arithmetic sequence is -16
ANSWER:
Arithmetic Sequence
Common difference
Recursive formula:
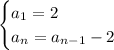
Explicit formula: