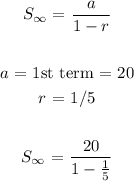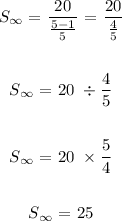Question

QUESTION 13. I neeed help with 13 only please explain step by step

Answer 1

Answer:

The sum of infinite geometric series is 25

Step-by-step explanation:

Given:

`13)\text{ }Geometric\text{ series: }20,\text{ 4, 4/5, . . .}`

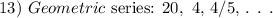
To find:

the sum of the infinite series if it diverges

An infinite series converger if -1 < r < 1

We need to check if the value of r values in the above interval

`\begin{gathered} common\text{ ratio = }\frac{next\text{ term}}{previous\text{ term}} \\ \\ common\text{ ratio = }(4)/(20)\text{ = 1/5} \\ \\ common\text{ ratio = }((4)/(5))/(4)\text{ = 1/5} \\ \\ (1)/(5)>\text{ -1 but less than 1 \lparen it falls in the interval\rparen} \\ Hence,\text{ it converges} \end{gathered}`

The sum of geometric infinite series is given as:

`\begin{gathered} S_(\infty)\text{ = }(a)/(1-r) \\ \\ a\text{ = 1st term = 20} \\ r\text{ = 1/5} \\ \\ S_(\infty)\text{ = }(20)/(1-(1)/(5)) \end{gathered}`
`\begin{gathered} S_(\infty)\text{ = }(20)/((5-1)/(5))\text{ = }(20)/((4)/(5)) \\ \\ S_(\infty)\text{ = 20 }/(4)/(5) \\ \\ S_(\infty)\text{ = 20 }*(5)/(4) \\ \\ S_(\infty)\text{ = 25} \end{gathered}`