we have the function
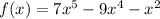
Simplify the expression
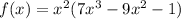
Find out the value of f(x) at x=1
For x=1
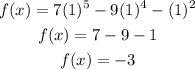
Find out the value of f(x) at x=2
For x=2
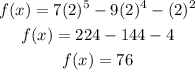
Note that
For x=1 --------> f(x) is negative
For x=2 ------> f(x) is positive
that means
between the interval (1,2) the graph cross the x-axis
that means
The given function has at least one real zeros between x=1 and x=2