Question

Gwen has &41.70 in her piggy bank. She has one more than three times as many dimes as she has nickels and she has five times as many quarters as nickels. How many of each coin does he have ?

Answer 1

Let x be the number of nickels.

We know that we have one more than three times as many dimes as nickels, the number of nickels can be express as:

`3x+1`

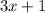
We also know that she has five times as many quartes, this can be express as:

`5x`

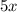
Now, we also know that in total she has $41.70 then we have the equation:

`0.05x+0.1(3x+1)+0.25(5x)=41.70`

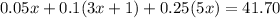
Solving for x we have:

`\begin{gathered} 0.05x+0.1(3x+1)+0.25(5x)=41.70 \\ 0.05x+0.3x+0.1+1.25x=41.70 \\ 1.6x+0.1=41.70 \\ 1.6x=41.70-0.1 \\ 1.6x=41.6 \\ x=(41.6)/(1.6) \\ x=26 \end{gathered}`

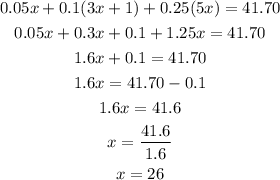
Now that we have the value of x we can plug it in the expression for the number of each type of coin.

For the nickels we have:

`3(26)+1=79`

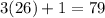
For the dimes we have:

`5(26)=130`

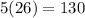
Therefore we have 26 nickels, 79 dimes and 130 quartes.