1 Answer

Vitomadio · Answer 1 · 2023-10-23T14:51:21+0000

Answer:

The limit is 1/5

Step-by-step explanation:

Given the function:

$\frac{\sqrt[]{x^2+24}-5}{x-1}$

Taking this limit as x approaches 1, we have:

$\begin{gathered} \frac{\sqrt[]{1^2+24}-5}{1-1}=\frac{\sqrt[]{25}-5}{1-1} \\ \\ (5-5)/(1-1)=(0)/(0) \end{gathered}$

This result means we need to apply a different method.

We apply L'hopital's rule, by taking the derivatives of the numerator and denominator as follows:

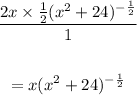
$\begin{gathered} \frac{2x*(1)/(2)(x^2+24)^{-(1)/(2)}}{1} \\ \\ =x(x^2+24)^{-(1)/(2)} \end{gathered}$

Now, taking the limit as x approaches 1, we have:

$\begin{gathered} 1(1^2+24)^{-(1)/(2)} \\ \\ =\frac{1}{\sqrt[]{25}}=(1)/(5) \end{gathered}$

Please log in or register to add a comment.