Answer:
The limit is 1/5
Step-by-step explanation:
Given the function:
![\frac{\sqrt[]{x^2+24}-5}{x-1}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1kakntmy1x6nc4yq0h3q637m9ighd1v5lk.png)
Taking this limit as x approaches 1, we have:
![\begin{gathered} \frac{\sqrt[]{1^2+24}-5}{1-1}=\frac{\sqrt[]{25}-5}{1-1} \\ \\ (5-5)/(1-1)=(0)/(0) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ko209l313ykycxh88samjme315s27jpo2u.png)
This result means we need to apply a different method.
We apply L'hopital's rule, by taking the derivatives of the numerator and denominator as follows:
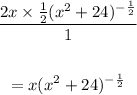
Now, taking the limit as x approaches 1, we have:
![\begin{gathered} 1(1^2+24)^{-(1)/(2)} \\ \\ =\frac{1}{\sqrt[]{25}}=(1)/(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/i9nenjaofc98i75u769y72kwaw8vxxh91v.png)