Question

Suppose that the weight (in pounds) of an airplane is a linear function of the total amount of fuel (in gallons) in its tank. When graphed, the function gives a linewith a slope of 5.5. See the figure below.With 52 gallons of fuel in its tank, the airplane has a weight of 2386 pounds. What is the weight of the plane with 81 gallons of fuel in its tank?

Answer 1

To determine the weight of the plane with 81 gallons of fuel, the first step is to determine the equation of the line:

We know that the slope of the line is m=5.5 and an ordered pair (52,2386)

Using the slope-intercept form, the first step is to replace the slope in the expression:

`\begin{gathered} y=mx+b \\ y=5.5x+b \end{gathered}`

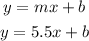
Next, replace the x and y values of the known ordered pair, this way, the y-intercept will be the only unknown term of the equation:

`\begin{gathered} 2386=5.5\cdot52+b \\ 2386=286+b \end{gathered}`

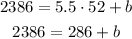
Subtract 286 from both sides of the equal sign to calculate the value of b:

`\begin{gathered} 2386-286=286-286+b \\ 2100=b \end{gathered}`

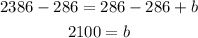
Now we know that the y-intercept is b=2100pounds (this is the weight of the plane when its tanks are empty)

The equation of the line is:

`y=5.5x+2100`

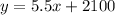
Now we can determine the weight of the place with x=81 gallons of fuel:

`\begin{gathered} y=5.5x+2100 \\ y=5.5\cdot81+2100 \\ y=445.5+2100 \\ y=2545.5 \end{gathered}`

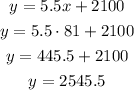
With 81 gallons of fuel, the weight of the plane will be 2545.5 pounds