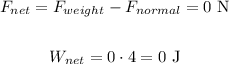Question

Gabrielle and Pierre are trying to move a 52 kg box by pushing it across the floor. Gabrielle is pushing with a force of 40 N [east], while Pierre is pushing with a force of 32 N [west]. There is also a friction force of 3 N [west] on the box. Assume the box travels 4 m [east].D. Remember that net force indicates an acceleration. In which direction is the box accelerating (and hence, moving)?E. Determine the work Gabrielle exerts on the box. Considering the direction the box is going, is the work positive or negative?F. Determine the work Pierre exerts on the box. Considering the direction the box is going, is the work positive or negative?G. Determine the work friction is doing on the box. Considering the direction the box is going, is the work positive or negative?H. Add together Gabrielle’s and Pierre’s work, and the work from the force of friction. If any of the amounts of work were negative, the amount becomes a negative number in the summation. I. What is the net work being done on the box in the horizontal direction?J. What is the net work being done on the box in the vertical direction?

Answer 1

D.

Since the net force is pointing east, the resulting acceleration is also pointing east.

E.

The work can be calculated with the formula below:

`W=F\cdot d`

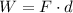
Since Gabrielle's force is to the east (same direction of the acceleration), so let's use a positive force:

`W=40\cdot4=160\text{ J}`

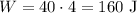
This work is positive.

F.

Pierre pushes the box in the opposite direction the box is moving, so his force is negative:

`W=-32\cdot4=-128\text{ J}`

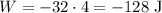
G.

The friction force is acting on the opposite direction of the movement, so it is negative:

`W=-3\cdot4=-12\text{ J}`

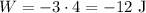
H.

adding all works, we have:

`160-128-12=20\text{ J}`

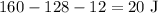
I.

To find the net work in horizontal, let's use the net force in horizontal:

`\begin{gathered} F_(net)=40-32-3=5\text{ N}\\ \\ W_(net)=5\cdot4=20\text{ J} \end{gathered}`

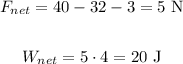
J.

To find the net work in vertical, let's use the net force in vertical:

`\begin{gathered} F_(net)=F_(weight)-F_(normal)=0\text{ N}\\ \\ W_(net)=0\cdot4=0\text{ J} \end{gathered}`