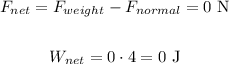D.
Since the net force is pointing east, the resulting acceleration is also pointing east.
E.
The work can be calculated with the formula below:

Since Gabrielle's force is to the east (same direction of the acceleration), so let's use a positive force:
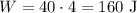
This work is positive.
F.
Pierre pushes the box in the opposite direction the box is moving, so his force is negative:
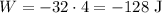
G.
The friction force is acting on the opposite direction of the movement, so it is negative:
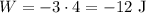
H.
adding all works, we have:
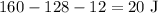
I.
To find the net work in horizontal, let's use the net force in horizontal:
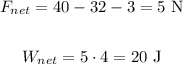
J.
To find the net work in vertical, let's use the net force in vertical: