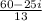Question

Perform the operation and write your answer in standard form.(2−3)(5)/2+3

Answer 1

Our problem involves operation of complex numbers. When dealing with complex number specially imaginary numbers (the one with an "i" ). We must remember that i² = -1.

So let us start.

`((2-3i)(5i))/((2+3i))`

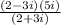
Step 1. Rationalize the denominator by multiplying both the numerator and denominator by (2 - 3i ), in order for us to get rid of the "i" in our denominator.

`((2-3i)(5i))/((2+3i))\cdot((2-3i))/((2-3i))=((2-3i)(5i)(2-3i))/((2+3i)(2-3i))`

*Notice that our denominator is just the SUM and DIFFERENCE of a SQUARE, therefore it will now become,

`\begin{gathered} ((2-3i)(5i)(2-3i))/((2+3i)(2-3i))=((2-3i)(5i)(2-3i))/(2^2-3^2(i^2))=\frac{(2-3i)(5i)(2-3i)}{4-9(-1)_{}_{}_{}} \\ =((2-3i)(5i)(2-3i))/(13) \end{gathered}`

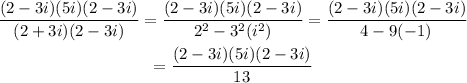
STEP 2. Now that we've settled our denominator let us now proceed to the numerator.

`((2-3i)(5i)(2-3i))/(13)=((2-3i)^2(5i))/(13)=\frac{(4-12i+9i^2)^{}(5i)}{13}`
`=\frac{(4-12i+9(-1)^{})^{}(5i)}{13}=\frac{(-5-12i)^{}(5i)}{13}`

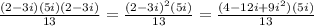
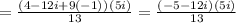
Now let us distribute 5i to the (-5 - 12i),

`\frac{(-5-12i)^{}(5i)}{13}=\frac{(-25i-60i^2)^{}}{13}=\frac{(-25i-60(-1))^{}}{13}`
`\frac{(-25i-60(-1))^{}}{13}=(60-25i)/(13)`

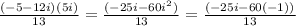
Therefore the answer for our operation is:

`(60-25i)/(13)`