To answer this question, we will use the following general form of an exponential model:
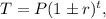
where P is the initial amount, r is the rate in decimal form, and t is the time.
In this case, since the herbicide degrades, the sign inside the parenthesis will be a minus sign, P=200, r=0.11, and t will be the time in weeks, therefore the number of gallons after t weeks can be modeled by the following equation:

Evaluating the above equation at t=2, we get:
(Answer part 1)
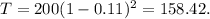
If we set T=50, and solve for t, we get:
(Answer part 2)
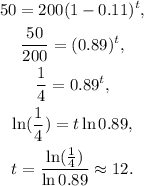
Answer:
There will be 158 gallons after 2 weeks.
In about 12 weeks the landscaper has to put another dose.