Answer:
• 3. 0.35
,
• 4. 0.6
,
• 5. 19/22
,
• 6. 7/13
,
• 7. 0.56
,
• 8. 0.6
,
• 9. 0.87
Explanation:
Part 3
The total number of students = 100
• The number of students who had a grade of A = 20
,
• The number of students who had a grade of B = 15
The probability that a randomly selected student got an A or B:
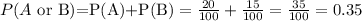
The probability that a randomly selected student got an A or B is 0.35.
Part 4
The number of male students who scored an A = 12.
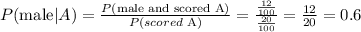
The probability that an "A" student is male is 0.6.
Part 5
The passing grades are A, B, C, and D.
• The number of females who had a passing grade = 8+9+13+8 = 38
• The number of females = 44
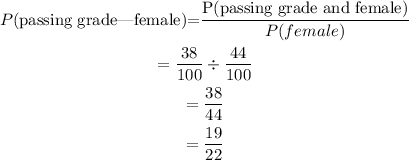
The probability that if a student was female that they got a passing grade is 19/22.
Part 6
The probability of a male student given that they failed.
• The number of students who failed = 7+6 = 13
,
• The number of male students who failed = 7
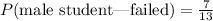
The probability of a male student given that they failed is 7/13.
Part 7
• The total number of students = 100
,
• The number of male students = 56.
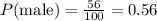
The probability of a randomly selected student being male is 0.56.
Part 8
• The number of female students that got a B = 9.
,
• The number of students that got a B = 15
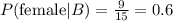
The probability of a female student given that they got a "B" is 0.6.
Part 9
The number of students who passed Mrs. Hardcase's class = 100-13=87
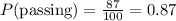
The probability of a randomly selected student passing Mrs. Hardcase's class is 0.87.