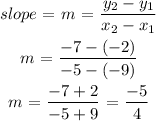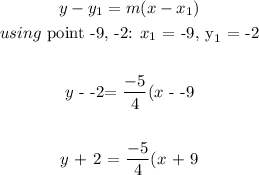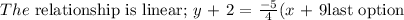Question

9. Is the relationship shown by the data linear? If so, model the data with an equation.IXby-2|-7-9-5-13F-12-17The relationship is not linear.The relationship is linear, y + 2 = (x + 9).The relationship is linear, y + 9 = -(x + 2).---(x + 2).OThe relationship is linear, y + 2 = -(x + 9).2 )

Answer 1

Answer:
`The\text{ relationship is linear; }y\text{ + 2 = }(-5)/(4)(x\text{ + 9\rparen \lparen last option\rparen}`

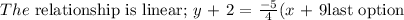Step-by-step explanation:

Given:

Table having x and y values

To find:

If the table is a linear one and model the equation if it

For a table to be linear, the change in x values will be constant and the change in y values will also be constant.

change in x:

-5-(-9) = -5 +9 = 4

-1-(-5) = -1 + 5 = 4

change in y:

-7 - (-2) = -7+2 = -5

-17 - (-12) = -17 + 12 = -5

The change in x and change in y have a constant value.

Hence, the relationship is linear

From the option, the equation is written in point-slope form, so we will use the point-slope formula to get our equation

`\begin{gathered} Point\text{ slope:} \\ $$y-y_1=m(x-x_1)$$ \end{gathered}`

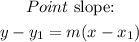
To get the slope, we will pick any two points on the table. Using points (-9, -2) and (-5, -7)

`\begin{gathered} slope\text{ = }m\text{ = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }(-7-(-2))/(-5-(-9)) \\ m\text{ = }(-7+2)/(-5+9)\text{ = }(-5)/(4) \end{gathered}`
`\begin{gathered} $$y-y_1=m(x-x_1)$$ \\ using\text{ point \lparen-9, -2\rparen: }x_1\text{ = -9, y}_1\text{ = -2} \\ \\ y\text{ - \lparen-2\rparen = }(-5)/(4)(x\text{ - \lparen-9\rparen\rparen} \\ \\ y\text{ + 2 = }(-5)/(4)(x\text{ + 9\rparen} \end{gathered}`

`The\text{ relationship is linear; }y\text{ + 2 = }(-5)/(4)(x\text{ + 9\rparen \lparen last option\rparen}`