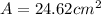We are given a rhombus with one side measuring 5 cm, and one angle measuring 50 degrees. To determine the area we can use the following formula:
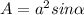
Where "a" is one side and alpha is the measure of any interior angle of the rhombus. In this case, we have that
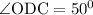
Since line DB bisects the angle ADC, that means that:
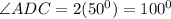
Replacing in the formula for the area:
![A=(5\operatorname{cm})^2\sin 100]()
Solving we get: