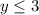Step-by-step explanation
The range of a function is a set composed of all of its output values. In this case this means all the possible y-values that the function can take. This is a cuadratic function which means that it has either a minimum or a maximum y-value that delimits its range. The sign of its leading coefficient is - which implies that this function has a maximum. This maximum is also known as the vertex of the function and if it's the point (h,k) then the range of this function can be described with this inequality:
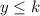
So if we find the y-value of the vertex we find the range. In order to find it we could find its x-value first. If the function has two x-intercepts then the x-value of the vertex is the midvalue of these two. Then we should find the x-intercepts so we find the x-value of the vertex and with it its y-value.
For any given quadratic equation of the form ax²+bx+c=0 its x-intercepts are given by:
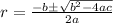
In our case we have a=-3, b=30 and c=-72 so we get:
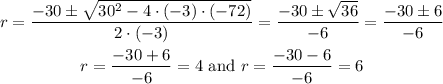
So the x-values of the x-intercepts are 4 and 6. Then the x-value of the vertex (h) of this function is:
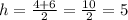
Then the y-value of the vertex k is given by taking x=5 in the equation:
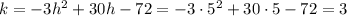
Answer
Then the answer is: