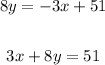Given the points ( 1 , 6 ) and ( 9 , 3 )
The slope of the line = m

so, the equation will be :

where b is a constant, we will find the value of b using the point ( 1 , 6 )
when x = 1 , y = 6
so,
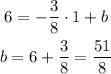
so, the equation of the line is:
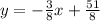
The standard form of the line will be as following:
Multiply the equation by 8
So,