Question

Solve 2 x x − =− 6 5 by completing the square.Show all work for the steps below.(a) For 2 x xc c − + =− + 6 5 , what value of c is used to complete the square? (b) Substitute the value for c in Part 2(a). Then complete the square to rewrite the equation as the square of a binomial. (c) Solve for x.can you walk me through this one?

Answer 1

Part a. We are given the following quadratic equation:

`x^2-6x=-5`

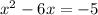
This is an equation of the form:

`x^2+bx=c`

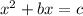
To complete the square we will add and subtract the following term:

`((b)/(2))^2`

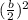
Substituting we get:

`((-6)/(2))^2`

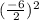
Solving the operations and simplifying we get:

`((-6)/(2))^2=(-3)^2=9`

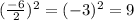
Therefore, the value of "c" is 9.

Part b. We will substitute the value of "c" in the equation:

`x^2-6x+9=-5+9`

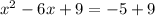
Now, we solve the operation on the right side:

`x^2-6x+9=4`

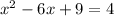
Now, we will factor the left side using the square of a binomial. Therefore, we take the square root of the first and third term and rearrange them in the form of the square of a binomial, like this:

`(x-3)^2=4`

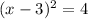
This completes part B.

Part C. Now, we will solve for "x". To do that we will take the square root to both sides:

`\begin{gathered} x-3=\sqrt[]{4} \\ x-3=\pm2 \end{gathered}`

Now we add 3 to both sides:

`x=3\pm2`

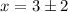
Since we have a quadratic equation there are two possible solutions for "x". The first solution is determined using the plus sign:

`x=3+2=5`

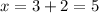
The second solution is determined using the minus sign:

`x=3-2=1`

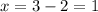
Therefore, the values of "x" are 5 and 1.