Part a. We are given the following quadratic equation:
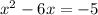
This is an equation of the form:
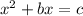
To complete the square we will add and subtract the following term:
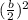
Substituting we get:
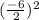
Solving the operations and simplifying we get:

Therefore, the value of "c" is 9.
Part b. We will substitute the value of "c" in the equation:
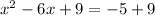
Now, we solve the operation on the right side:
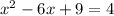
Now, we will factor the left side using the square of a binomial. Therefore, we take the square root of the first and third term and rearrange them in the form of the square of a binomial, like this:

This completes part B.
Part C. Now, we will solve for "x". To do that we will take the square root to both sides:
![\begin{gathered} x-3=\sqrt[]{4} \\ x-3=\pm2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8zaktst2idut7lt6v7aivl0fud7ivwybw0.png)
Now we add 3 to both sides:
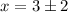
Since we have a quadratic equation there are two possible solutions for "x". The first solution is determined using the plus sign:
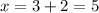
The second solution is determined using the minus sign:
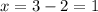
Therefore, the values of "x" are 5 and 1.