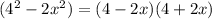The simplify an expression as a frection, we need to find eqaul terms in the nominator and denominator, to cancell them. The idea is, if we have a number called n, and a expression like:
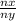
We can divide n by n in order to get a simplifyed expression.
In this case we have:
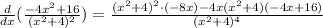
We can see that the term (x² + 4) is repeated in the numerator and denominator. To do this easier, let's separate this in a sum of fractions:
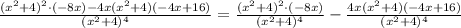
Now it's much easier to cancell the repeated terms:
In the first fraction, we have the parentheses squared in the numerator and power of 4 in the denominator, to divide it, we can use the power propierties:
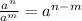
Then:
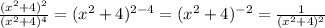
And now the first fraction is:
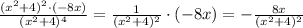
For the second fraction is very similar:
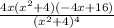
We have the same term (x² + 4) , in the numerator and denominator. Then divide:
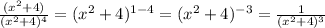
Then the second fraction is:
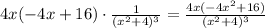
Now we can add the two fraction to get the final asnwer:
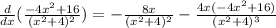
And that's all the simplifying we can do with this derivative
If we look at the second fraction, we have a difference of squares:
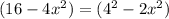
Thus: