SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given question.
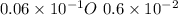
STEP 2: Divide the expression into two parts and solve each parts to get their results
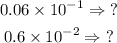
STEP 3: Solve the first expression

STEP 4: Solve the second expression

STEP 5: Compare the two results from the simplified expressions
![\begin{gathered} \text{0}.006\Rightarrow0.006 \\ It\text{ can be se}en\text{ that the expression on the right hand side is equal to the expression on the left hand side} \end{gathered}]()
Hence,
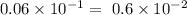
Equal sign(=)