Question

This is my first time with this type of question so I really don’t understand it

Answer 1

This question is asking about the value of the angle that gives us a sine of 4/15.

To find this angle, we need to use the inverse function of the sine function which is called arcsin function, and it is also represented as:

`\arcsin (x)=\sin ^(-1)(x)`

Then, to find the angle, we need to apply the latter function on both sides of the equation as follows:

`\arcsin (\sin (x^(\circ)))=\arcsin ((4)/(15))=\sin ^(-1)((4)/(15))=15.4660099534`

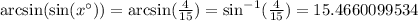
We need to be careful that the value that gives us a calculator is in degrees (as in this case).

If we round the answer to the nearest tenth, we finally have that:

`\arcsin (\sin (x^(\circ))=x^(\circ)=15.5`

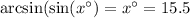
In summary, the value for angle x° is equal to 15.5° (third option).