Question

Find the equation of the line through the point (1,-4) that is parallel to the line with equation -13x-3y=-66

Answer 1

Given:

A line is passing through the point (1, -4) and parallel to the line

`-13x-3y=-66`

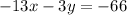
To find:

The equation of the line.

Step-by-step explanation:

Let us write the given equation in the slope-intercept form,

`\begin{gathered} -3y=13x-66 \\ y=-(13)/(3)x+22 \end{gathered}`

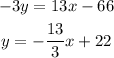
So, the slope of the line is,

`m=-(13)/(3)`

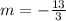
Since the lines are parallel. So, the slopes are equal.

Using the point and slope formula,

`\begin{gathered} (y-y_1)=m(x-x_1) \\ (y-(-4))=-(13)/(3)(x-1) \\ y+4=-(13)/(3)x+(13)/(3) \\ y=-(13)/(3)x+(13)/(3)-4 \\ y=-(13)/(3)x+(1)/(3) \\ y=(-13x+1)/(3) \\ 3y=-13x+1 \\ 13x+3y-1=0 \end{gathered}`

Therefore, the equation of the line is,

`13x+3y-1=0`

Final answer:

The equation of the line is,

`13x+3y-1=0`