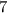We will investigate the manipulation of arithmatic sequences expressed as general nth terms.
An arithmatic sequences are expressed as following:
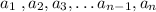
Where,

An arithmatic sequence is defined by two parameters:
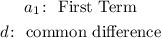
Where,
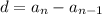
The general formulation of the nth term in a arithmatic sequence is as follows:
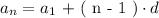
We are given the following arithmatic sequence terms:
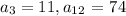
We are to determine the common difference ( d ) for the above sequence. We will use the general formulation to construct equations:
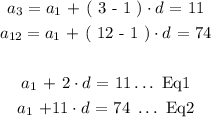
We will solve the above two equations simultaneosuly:
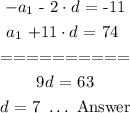
The common difference for the above sequence is: