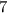Question

Find the common difference in the arithmetic sequence, an, in which a3=11 and a12=74.

Answer 1

We will investigate the manipulation of arithmatic sequences expressed as general nth terms.

An arithmatic sequences are expressed as following:

`a_{1\text{ }},a_2,a_3,\ldots a_(n-1),a_n`

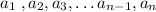
Where,

`\begin{gathered} a_1\colon FirstTerm_{} \\ a_n\colon\text{ nth Term} \\ n\colon\text{ Term number} \end{gathered}`

An arithmatic sequence is defined by two parameters:

`\begin{gathered} a_1\colon\text{ First Term} \\ d\colon\text{ common difference} \end{gathered}`

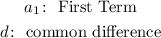
Where,

`d=a_n-a_(n-1)`

The general formulation of the nth term in a arithmatic sequence is as follows:

`a_n=a_1\text{ + ( n - 1 )}\cdot d`

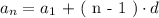
We are given the following arithmatic sequence terms:

`a_3=11,a_(12)\text{ = }74`

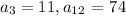
We are to determine the common difference ( d ) for the above sequence. We will use the general formulation to construct equations:

`\begin{gathered} a_3=a_1\text{ + ( 3 - 1 )}\cdot d\text{ = }11 \\ a_(12)=a_1\text{ + ( 12 - 1 )}\cdot d\text{ = 74} \\ \\ a_1\text{ + 2}\cdot d\text{ = }11\ldots\text{ Eq1} \\ a_1\text{ +11}\cdot d\text{ = 74 }\ldots\text{ Eq2} \end{gathered}`

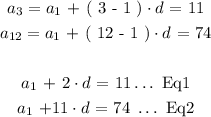
We will solve the above two equations simultaneosuly:

`\begin{gathered} -a_1\text{ - 2}\cdot d\text{ = -}11 \\ a_1\text{ +11}\cdot d\text{ = 74 } \\ ========== \\ 9d\text{ = 63} \\ d\text{ = 7 }\ldots\text{ Answer} \\ \end{gathered}`

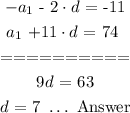
The common difference for the above sequence is:

`7`