a) From the graph, we see that the function takes the value y = 4 when x = 4, so we have:
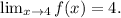
b) We see that the curve tends to -∞ when x approaches zero from the left, so we have:
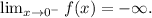
c) We see that curve increases without limit when x tends to infinity, so we have:
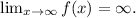
d) From the graph, we see that the function tends to y = 0 when x approaches zero from the right, so we have:
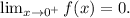
e) Yes, there are two possible values of x for the limit of the function approaching 4:
• x = 2,
,
• x = 4.
By definition, a function is continuous when its graph is a single unbroken curve.
We see that at the points x = 2 and x = 4 the curve is a single unbroken curve, so we conclude that the function is continuous at those points.
Answers
a, b, c, d
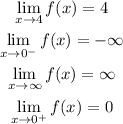
e. Yes, there are two possible values of x for the limit of the function approaching 4:
• x = 2,
,
• x = 4.
By definition, a function is continuous when its graph is a single unbroken curve.
We see that at the points x = 2 and x = 4 the curve is a single unbroken curve, so we conclude that the function is continuous at those points.