Question

Part 2: Write limits given outputs.Use the graph of the function to write limit equations given limit values.Use the graph to write a limit equation for f(x) that satisfies each given condition. (2 points for each)a. b. c. d. e. Are there other values than what you chose for x where the limit of the function approaches 4? Is the graph continuous at these points? Explain your reasoning. (4 points)

Answer 1

a) From the graph, we see that the function takes the value y = 4 when x = 4, so we have:

`\lim _(x\rightarrow4)f(x)=4.`

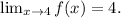
b) We see that the curve tends to -∞ when x approaches zero from the left, so we have:

`\lim _(x\rightarrow0^-)f(x)=-\infty.`

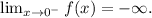
c) We see that curve increases without limit when x tends to infinity, so we have:

`\lim _(x\rightarrow\infty)f(x)=\infty.`

d) From the graph, we see that the function tends to y = 0 when x approaches zero from the right, so we have:

`\lim _(x\rightarrow0^+)f(x)=0.`

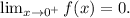
e) Yes, there are two possible values of x for the limit of the function approaching 4:

• x = 2,

,

• x = 4.

By definition, a function is continuous when its graph is a single unbroken curve.

We see that at the points x = 2 and x = 4 the curve is a single unbroken curve, so we conclude that the function is continuous at those points.

Answers

a, b, c, d

`\begin{gathered} \lim _(x\rightarrow4)f(x)=4 \\ \lim _(x\rightarrow0^-)f(x)=-\infty \\ \lim _(x\rightarrow\infty)f(x)=\infty \\ \lim _(x\rightarrow0^+)f(x)=0 \end{gathered}`

e. Yes, there are two possible values of x for the limit of the function approaching 4:

• x = 2,

,

• x = 4.

By definition, a function is continuous when its graph is a single unbroken curve.

We see that at the points x = 2 and x = 4 the curve is a single unbroken curve, so we conclude that the function is continuous at those points.