Question

A complex number zı has a magnitude z1] = 2 and an angle 6, = 49°.=Express zy in rectangular form, as 21 == a +bi.Round a and b to the nearest thousandth.21 =+iShow Calculator

Answer 1

Complex numbers can be written in two forms:

`\begin{gathered} z=a+b\cdot i \\ z=r\cdot e^(i\theta) \end{gathered}`

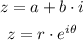
Where a and b are known as the real and the imaginary part and r and theta are the magnitude and the angle of the number. In this case we are given these last two quantities and we have to find a and b. One way to do this is recalling an important property of the exponential expression above:

`e^(i\theta)=\cos \theta+i\sin \theta`

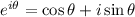
Then the exponential form of a number is equal to:

`z=r\cdot e^(i\theta)=r\cdot(\cos \theta+i\sin \theta)=r\cos \theta+i\cdot r\sin \theta`

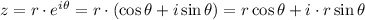
And since we are talking about the same number then this expression must be equal to that given by a and b:

`a+i\cdot b=r\cos \theta+i\cdot r\sin \theta`

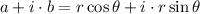
Equalizing terms without i and those with i we have two equations:

`\begin{gathered} a=r\cos \theta \\ b=r\sin \theta \end{gathered}`

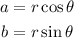
Now let's use the data from the exercise:

`\begin{gathered} r=\lvert z_1\rvert=2 \\ \theta=\theta_1=49^(\circ) \end{gathered}`

Then we have:

`\begin{gathered} a=2\cdot\cos 49^(\circ) \\ b=2\cdot\sin 49^(\circ) \end{gathered}`

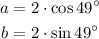
Using a calculator we can find a and b:

`\begin{gathered} a=1.312 \\ b=1.509 \end{gathered}`

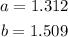
Then the answers for the two boxes are 1.312 and 1.509