b)
Given:
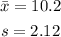
Hence,

So, the measurements in the data between 8.08 and 12.32 are 11, 9, 12, 10 12, 12 , 12, 9, 9, 9, 11, 11, 12 and 11.
Therefore, the number of measurements in interval x±s is 14.
The percentage of the measurements that fall between the interval x±s is,
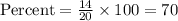
Therefore, the percentage of the measurements that fall between the interval x±s is 70%.
Now,
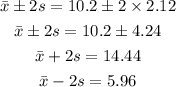
So, all the measurements in the data are between 5.96 and 14.44.Therefore, the number of measurements in interval x±2s is 20.
Therefore, the percentage of the measurements that fall between the interval x±2s is 100%.
Now,
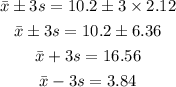
So, all the measurements in the data are between 3.84 and 16.56.Therefore, the number of measurements in interval x±3s is 20.
Therefore, the percentage of the measurements that fall between the interval x±3s is 100%.
Last part: compare the percentage .
According to empirical rule, approximately 68% of the measurements in a sample will fall within the interval x±s.
From part b, the obtained percentage of measurements that fall within the interval x±s is 70%.
Therefore, percentage of measurements that fall within the interval x±s is greater than the predicted percentage for x±s using the empirical rule.
Option C is correct.