Question

Graph the system of quadratic Inequalities. (please show how you find the points to graph)

Answer 1

`\begin{gathered} x^2-4x+8>y \\ -x^2+4x+2\le y \end{gathered}`

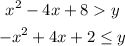
Points you need to find to graph quadratic inequalities:

Vertex of each parabola:

1-Write each ineqaulity as an equation:

`\begin{gathered} y=x^2-4x+8 \\ y=-x^2+4x+2 \end{gathered}`

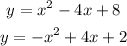
Vertex:

`\begin{gathered} f(x)=ax^2+bx+c \\ x-coordinate\text{ of the vertex:} \\ x=-(b)/(2a) \\ \\ y-coordinate\text{ of the vertex:} \\ f(-(b)/(2a)) \end{gathered}`

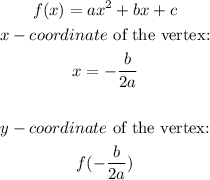
First equation: the leding coefficient is 1 then the parabola opens up.

Vertex of first equation:

`\begin{gathered} x=-(-4)/(2(1))=(4)/(2)=2 \\ \\ y=2^2-4(2)+8 \\ y=4-8+8 \\ y=4 \\ \\ \text{Vertex: (2,4)} \end{gathered}`

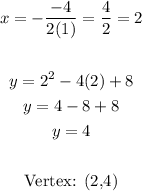
Second equation: the leading coefficient is -1 then the parabola opens down.

Vertex of the second equation:

`\begin{gathered} x=-(4)/(2(-1))=(-4)/(-2)=2 \\ \\ \\ y=-(2)^2+4(2)+2 \\ y=-4+8+2 \\ y=6 \\ \\ \text{Vertex: (2,6)} \end{gathered}`

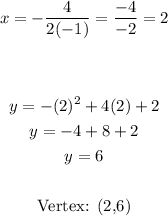
Points of interception:

Equal the equations and solve x:

`\begin{gathered} x^2-4x+8=-x^2+4x+2 \\ \\ x^2+x^2-4x-4x+8-2=0 \\ 2x^2-8x+6=0 \\ \\ \text{Quadratic formula:} \\ ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ \\ x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(2)(6)}}{2(2)} \\ \\ x=\frac{8\pm\sqrt[]{64-48}}{4} \\ \\ x=\frac{8\pm\sqrt[]{16}}{4} \\ \\ x=(8\pm4)/(4) \\ \\ x_1=(8+4)/(4)=(12)/(4)=3 \\ \\ x_2=(8-4)/(4)=(4)/(4)=1 \end{gathered}`

The parabolas intersect in x=1 and x=3 (use one of the equations to find the y-value of the intersection):

`\begin{gathered} y=1^2-4(1)+8 \\ y=1-4+8 \\ y=5 \\ \\ \text{point: (1,5)} \\ \\ y=3^2-4(3)+8 \\ y=9-12+8 \\ y=5 \\ \\ \text{point: (3,5)} \end{gathered}`

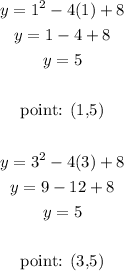
Then, you have the next points:

Vertex: (2,4) opens up; (2,6) opens down

Intersection points: (1,5) and (3,5)

First parabola has the inequality sing > : the border line is a dotted line and the shadow area is under the parabola.

Second parabola has the inequality sing ≤ : the border line is a full line and the shadow area is over the parabola

Graph: