Question

A book of mass m = 10kg is balanced on a table Determine the weight of the book and the component of the reaction of the table in each of the following cases: 1)The book is simply placed on the table2) Someone puts their hand on the book by exerting a vertical force of 40N3)Someone is pulling this book vertically upwards with a force of 40N

Answer 1

Given,

The mass of the book, m=10 kg

The weight of an object is given by the product of its mass and the acceleration due to gravity.

Thus the weight of the book is given by,

`W=mg`

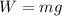
Where g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} W=10*9.8 \\ =98\text{ N} \end{gathered}`

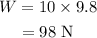
Therefore the weight of the book is 98 N

1)

When the book is placed on the table reaction of the table will be equal to the weight of the book. Thus, the reaction of the table, in this case, will be 98 N

2)

The vertically downward force applied on the book, F=40 N

The reaction of the table when there is a vertically downward force is equal to the sum of the weight and the applied force.

Thus the reaction of the table, in this case, is given by,

`N=W+F`

On substituting the known values,

`\begin{gathered} N=98+40 \\ =138\text{ N} \end{gathered}`

Thus, the reaction of the table when a vertically downward force is acting on it is 138 N

3)

The vertically upward force acting on the book, F=40 N

As the book is in equilibrium, the net force acting on the book must be equal to zero. That is total upward forces acting on the book must be equal to the total downward forces. Thus,

`\begin{gathered} N+F=W \\ \Rightarrow N=W-F \end{gathered}`

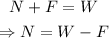
Where N is the normal force.

On substituting the known values,

`\begin{gathered} N=98-40 \\ =58\text{ N} \end{gathered}`

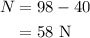
Thus the reaction of the table, in this case, is 58 N