Given: The information of a boat heading towards a lighthouse
To Determine: The distance from point A to point B
Solution: The information provided can be translated into the diagram below
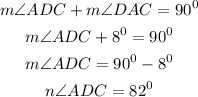

Using SOH CAH TOA
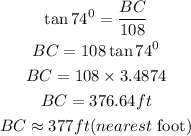
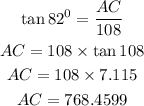
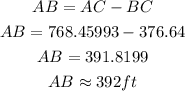
Hence, the distance from point A to point B is 392ft (nearest foot)