Given the functions:
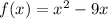

1) (f+g)(x) You have to calculate the sum between f(x) and g(x) for x=7
First, calculate the sum between both functions:
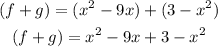
Order the like terms together and simplify:
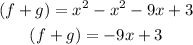
Substitute the expression with x=7 and solve:

The result is (f+g)(7)= -60
2) (f-g)(7) You have to calculate the difference between f(x) and g(x) for x=7
First, calculate the difference between both functions:
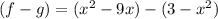
First, erase the parentheses, the minus sign before (3-x²) indicates that you have to change the sign of both terms inside the parentheses, as if they were multiplied by -1, then:
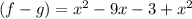
Order the like terms and simplify:
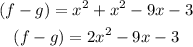
Substitute the expression with x=7 and solve:
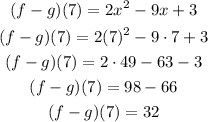
The result is (f-g)(7)= 32
3) (fg)(7) In this item you have to calculate the product of f(x) and g(x) for x=7
First, determine the product between both functions:
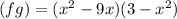
Multiply each term of the first parentheses with each term of the second parentheses:

Substitute with x=7 and solve:
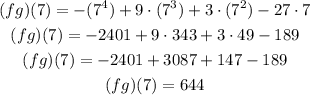
The result is (fg)(7)=644
4) (f/g)(7) First, divide both functions:
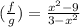
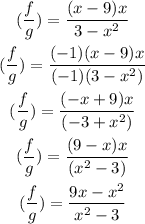
Substitute with x=7 and solve:
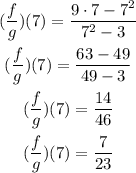
The result is (f/g)(7)= 7/23