Given the function:
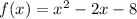
It is a quadratic function where:
a=1
b= -2
c= -8
The x-coordinate of the vertex is given by:
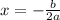
Substitute a and b:
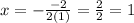
Substituting in the original equation to obtain the y-coordinate, we obtain:
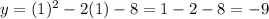
So, the vertex is (0, -9)
c. For the intercept at x we make y = 0:
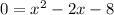
And solve for x by factorization:
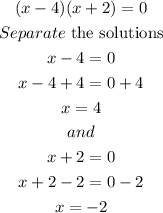
So, the x-intercepts are:
(-2, 0) and (4,0)
Answer: (-2,0), (4,0)
d. For the intercept at y we make x = 0:
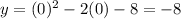
So the y-intercept is (0, -8)
Answer: (0, -8)
e. Graphing the function: