In order to find the minimum and maximum value in the given interval, first let's find the vertex coordinates:
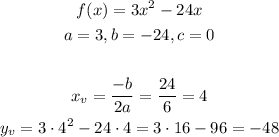
Since the coefficient a is positive, so the y-coordinate of the vertex is a minimum point, therefore the absolute minimum is (4,-48).
Then, to find the maximum, we need the x-coordinate that is further away from the vertex.
Since 0 is further away from 4 than 7, let's use x = 0:
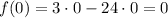
Therefore the absolute maximum is (0,0).