Question

Find the absolute extrema for the function on the given inveral

Answer 1

In order to find the minimum and maximum value in the given interval, first let's find the vertex coordinates:

`\begin{gathered} f(x)=3x^2-24x \\ a=3,b=-24,c=0 \\ \\ x_v=(-b)/(2a)=(24)/(6)=4 \\ y_v=3\cdot4^2-24\cdot4=3\cdot16-96=-48 \end{gathered}`

Since the coefficient a is positive, so the y-coordinate of the vertex is a minimum point, therefore the absolute minimum is (4,-48).

Then, to find the maximum, we need the x-coordinate that is further away from the vertex.

Since 0 is further away from 4 than 7, let's use x = 0:

`f(0)=3\cdot0-24\cdot0=0`

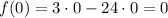
Therefore the absolute maximum is (0,0).