Since it is given that the population grows by 5% each year, it follows that the Exponential Growth Function is the appropriate function that can be used to model the problem.
The Exponential Growth Function is given by:
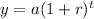
Where
• a is the initial amount.
,
• r is the percent of increase in decimal.
,
• t is the time.
,
• y is the amount after time t.
Since we want when the initial population will triple, substitute y=3a into the equation:
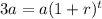
Substitute r=5%=0.05 into the equation:

Solve the resulting equation for t:
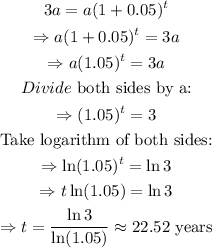
The population will triple after about 22.52 years.