First, notice that Ryan and its shadow form a right triangle with the following measures:
and with the tree, we have the following triangle:
since both triangles are similar, we can write the following proportions:
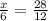
where 'x' represent the height of the tree. Solving for 'x', we get:
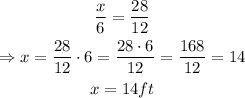
therefore, the height of the tree is 14 feet