Question

Ryan is 6 feet tall. At a certain time of day, he casts a shadow that is 12 feet long. At the same time, a tree casts ashadow that is 28 feet long. What is the height of the tree?

Answer 1

First, notice that Ryan and its shadow form a right triangle with the following measures:

and with the tree, we have the following triangle:

since both triangles are similar, we can write the following proportions:

`(x)/(6)=(28)/(12)`

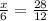
where 'x' represent the height of the tree. Solving for 'x', we get:

`\begin{gathered} (x)/(6)=(28)/(12) \\ \Rightarrow x=(28)/(12)\cdot6=(28\cdot6)/(12)=(168)/(12)=14 \\ x=14ft \end{gathered}`

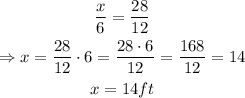
therefore, the height of the tree is 14 feet