Question

Is the following pair of vectors Parallel, Perpendicular/Orthogonal or Neither?m = < 1 , 5 > n = < 3 , 15 >

Answer 1

1) To find out we need to calculate the dot product of those two vectors

`\begin{gathered} m\cdot n=\mleft\langle1,5\mright\rangle\cdot\mleft\langle3,15\mright\rangle=1\cdot3+5\cdot15=3+75=78 \\ \end{gathered}`

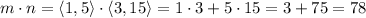
Since these vectors have a dot product different than zero, then they are not Orthogonal.

2) Let's now check if they are perpendicular, calculating the norm of each one and the angle between them:

`\begin{gathered} \mleft\|m\mright\|=\sqrt[]{1^2+5^2}=\sqrt[]{26} \\ \|n\|=\sqrt[]{3^2+15^2}=\sqrt[]{9+225}=\sqrt[]{234} \end{gathered}`

And finally the angle theta between them:

`\begin{gathered} \theta=\cos ^(-1)((u\cdot v)/(\|m\|\cdot\|n\|)) \\ \theta=\cos ^(-1)(\frac{78}{\sqrt[]{26}\cdot\sqrt[]{234}}) \\ \theta=0 \end{gathered}`

3) Since the angle is 0, these vectors are parallel since parallel vectors for 0º or 180º