1) To find out we need to calculate the dot product of those two vectors
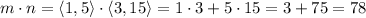
Since these vectors have a dot product different than zero, then they are not Orthogonal.
2) Let's now check if they are perpendicular, calculating the norm of each one and the angle between them:
![\begin{gathered} \mleft\|m\mright\|=\sqrt[]{1^2+5^2}=\sqrt[]{26} \\ \|n\|=\sqrt[]{3^2+15^2}=\sqrt[]{9+225}=\sqrt[]{234} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1ez638re1oq05gqq346cmbij9dj9eg0m7c.png)
And finally the angle theta between them:
![\begin{gathered} \theta=\cos ^(-1)((u\cdot v)/(\|m\|\cdot\|n\|)) \\ \theta=\cos ^(-1)(\frac{78}{\sqrt[]{26}\cdot\sqrt[]{234}}) \\ \theta=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gb4iprcte004g8aea6wsgx3w6znndrlr2b.png)
3) Since the angle is 0, these vectors are parallel since parallel vectors for 0º or 180º