Question

The number of newly reported crime cases in a county in New York State is shown inthe accompanying table, where x represents the number of years since 2006, and yrepresents number of new cases. Write the linear regression equation that representsthis set of data, rounding all coefficients to the nearest tenth. Using this equation,estimate the calendar year in which the number of new cases would reach 767.Years since 2006 (x) New Cases (y)099619232882389248405813

Answer 1

For this case we have the following data:

x y

0 996

1 923

2 882

3 892

4 840

5 813

sum xi = 15

sum yi = 5346

sum xi yi = 12788

sum xi^2 = 55

And we want to find and equation like this one:

y= mx+ b

So then we can estimate the slope using least squares and we have:

`m=(n\sum ^n_(i=1)x_iy_i-\sum ^n_(i=1)x_i\sum ^n_(i=1)y_i)/(n(\sum ^n_(i=1)x^2_i)-(\sum ^n_(i=1)x_i)^2)`

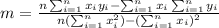
Replacing we have:

`m=(6\cdot12788-(15\cdot5346))/(6(55)-(15)^2)=(-3462)/(105)=-32.971`

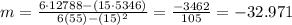
m= -32.971

And the intercept would be:

`b=(\sum^n_(i=1)y_i)/(n)-m\cdot(\sum^n_(i=1)x_i)/(n)=(5346)/(6)-(-32.971)\cdot(15)/(6)=973.429`

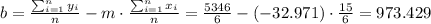
b= 973.428

Then the equation would be:

y= -32.971x+ 973.428

And we can find the value of x for y = 767 and we got::

767 = -32.971x+ 973.428

Solcing for x we have:

767- 973.428 = -32.971 x

x= 6.26

Regression Equation: y= -32.9x + 973.4

Final Answer: 2012