To write the vector s in the form s=ai + bj, we can use the next formula:
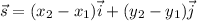
Where (x1,y1) are the coordinates of the initial point and (x2,y2) are the coordinates of the terminal point, by replacing these values we have:
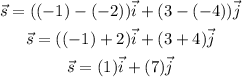
Then the vector s in the form s=ai+bj is: s= 1i + 7j