Answers:
Vertex: (4, -9)
axis of symmetry: x = 4
Domain: (-∞, ∞)
Range: [-9, ∞)
Step-by-step explanation:
If we have a quadratic function with the form y = ax² + bx + c, the x-coordinate of the vertex will be at x = -b/2a
So, for f(x) = x² - 8x + 7, we get a = 1, b = -8 and c = 7, then the x-coordinate of the vertex will be:
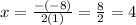
Then, the y-coordinate will be the value of f(x) when x = 4
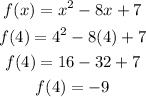
Therefore, the vertex of the equation is the point (x, y) = (4, -9).
The axis of symmetry is located in the vertex, since the parabola opens up, the axis of symmetry is the vertical line x = 4.
To graph the function, we need to find some points before and after the vertex. So, we will give values to x as 2, 3, 5, and 6. Then, we can calculate f(x) as:
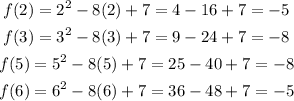
So, to graph the function, we will use the points (2, -5), (3, -8), (5, -8), (6, -5) and the vertex (4, -9). Therefore, the graph is:
Finally, the domain is the set of values that the variable x can take. In this case, x can be any number, so the domain is the set of all real numbers or written as an interval
(-∞, ∞)
And the range is the set of all values that f(x) can take. In this case, f(x) is always greater than -9, so the range is the set [-9, ∞)